Theoretical Breeding History of a Small Population
To get a clear idea of how such a change of allele frequency can happen, let's attempt to track a theoretical population's breeding history with reference to the B-locus. To keep things as simple as possible, we'll make some initial assumptions that will limit other variables. Assume that the breeding population consists of ten animals, that the animals in each generation are bred only once and then retired, that generations are separate and non-overlapping, and that from each filial generation another ten animals are selected for breeding.
In order to understand clearly what happens in the course of each generation's breeding and selection, we'll assume that we as observers know the actual genotype of every single animal, although the breeder herself cannot know the genotypes before selecting an animal or deciding upon a mating. We'll start with assumed allele frequencies of FB = 0.7, Fb = 0.3, and we'll assign genotypes to the individual animals as follows:
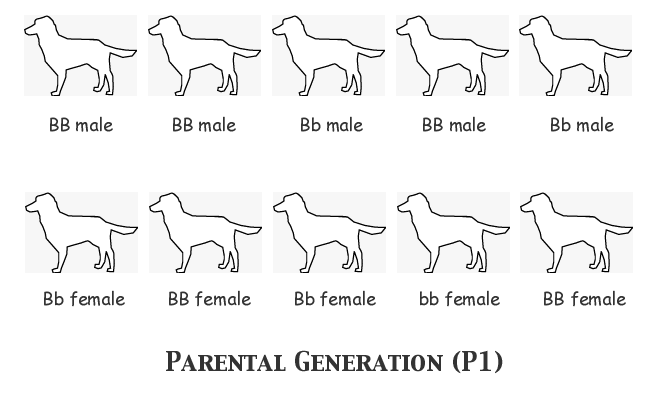
Notice that we have the correct number of each allele: 14 B and 6 b. Notice also that nine animals are black-nosed phenotype and only one is liver-nosed (bb). Now for the first filial generation the males in the top row will all be mated, each one to the female immediately below him in the bottom row. We'll just list the genotypes of the progeny in each litter:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
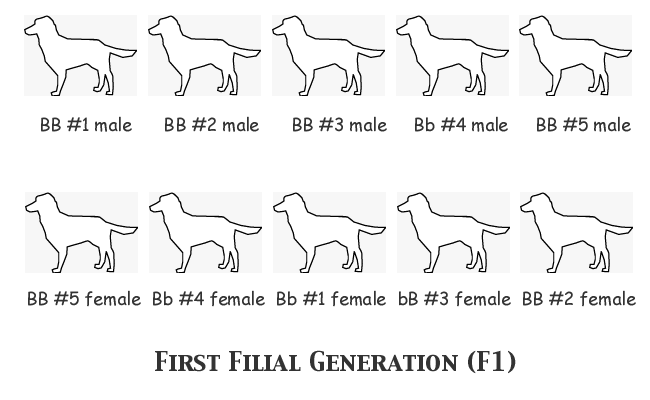
We got three litters of six pups each, one of three pups, and one of five. Twenty-six puppies. Let's keep the math easy by assuming that the female bb puppy in Litter #3 was a weakling that died in the nest, leaving us with 25 pups, so that 2N = 50. We have fifty copies of the B-locus gene in the F1 generation; counting up the two alleles, we find B = 40 and b = 10 (since we are concerned with the gene frequency of the surviving F1 population, we don't count the dead puppy's gene copies). But wait! That means that FB = 0.8 and Fb = 0.2! Let's look back and make sure there was nothing unusual about any of those litters. Litter #1 has exactly the distribution of genotypes that we should expect from a mating of BB x Bb -- three BB individuals and three Bb's. Nothing wrong there. Litter #2 consists entirely of BB puppies, but both the sire and the dam were homozygous BB genotypes, so that was all they could possibly produce. The theoretical expectation of genotypes for Litter #3 would be equal numbers of BB, Bb, bB, and bb; in this case, we certainly did get one of each of those genotypes, but the litter consisted of six puppies not four, and the two additional pups both happened to be BB homozygotes. This is the only litter that is in any way unusual, but the actual genotype distribution is not far enough from the expectation to be really improbable. Chalk this one up to sampling error. Litter #4 consists of three pups of the only possible genotype for that mating, all Bb heterozygotes. Litter #5's theoretical expectation is half BB homozygotes and half bB heterozygotes; we got just that, but the odd-numbered puppy, the lone female, turned out to be another BB (she might just as easily have had the bB genotype as the probability was a toss-up).
Of the five litters in the first filial generation, only one is the slightest bit unusual, and it was not at all an improbable result, just a deviation from the expected distribution of the kind that any breeder who knows her colour genetics has seen time and time again over the course of her breeding career. All the same, the resulting population of twenty-five growing puppies has a gene frequency that is measurably different from that of the parental generation. Also notice that we no longer have any liver-nosed animals in this generation; there was one such pup but it happened to be the one that died. Of the twenty-five survivors, the breeder has no way of knowing, before she selects them for breeding, which are BB homozygotes and which are Bb or bB heterozygotes; they all have the black-nose phenotype, so we cannot know until they have been bred which carry the b recessive. Even then, the only way to identify the heterozygotes for certain would be to test-breed every individual to a homozygote bb partner. (This is why the notion of test-breeding to identify carriers of dangerous recessive genes is a rather impractical proposition -- if the recessive is really a defective gene, you must produce litter after litter of puppies, half of which will be homozygous recessives, just to identify the carriers. Test-breeding works, as long as you aren't bothered about the humane considerations of breeding large numbers of defective animals that must then be euthanised.)
Now our breeder will select a male and a female from each of the five litters to breed the next generation. She won't mate any brothers and sisters, but otherwise there won't be any particular plan or pattern to these matings. Remember now, she has no way to identify which are the dominant homozygotes and which are heterozygotes carrying the recessive b gene.
Note that the gene frequency of the group selected is no different from that of the entire F1 population; B = 16 copies and b = 4 copies. There was no way to ensure that the breeder's selective reduction of the breeding population from a potential twenty-five to a realistic ten wouldn't change the allele frequencies; she might have selected a population with a higher number of B copies and fewer b copies, or it could have been the other way 'round. She can only see the phenotype, not the genotype, so chance plays its part in the final result. In this case, though, I don't want the reader saying that I deliberately loaded the dice in selecting for this example, so I have made sure that the gene frequency of the selection is representative of the entire group.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
To continue reading "Random Drift -- The Breeder's Hidden Enemy" click here.
